Dynamic Head
论文:Dynamic Head: Unifying Object Detection Heads with Attentions
Computer Vision and Pattern Recognition 2021
微软在2021年发表的这篇论文提出了新的dynamic head框架通过attention来统一目标检测head,通过连贯组合feature levels之间的尺度感知(Scale-awareness)、空间位置感知(Spatial-awareness)以及输出通道内的任务感知(Task-awareness)的多种自注意力机制,显著提高了检测头的表示能力,同时不产生任何计算开销。
-
Scale-awareness
特征金字塔已经成为现代目标检测器的标准组件。但是不同levels的特征通常是在下采样卷积网络的不同深度提取的,这会导致明显的语义差异。
-
Spatial-awareness
卷积网络在学习图像中存在的空间变换方面受到限制。
-
Task-awareness
对象特征的各种表示形式可以提高检测性能。
Method
本文将自注意力机制分开在三个维度:level-wise、spatial-wide、channel-wise,分别对应Scale-awareness、Spatial-awareness、Task-awareness,将三个维度上的注意力统一在一个head中。
对于来自特征金字塔的不同层级$L$的特征:$\mathcal{F} =\{F_{i}\}^{L}_{i=1}$,通过上采样或下采样调整连续级别特征的大小得到接近中间级别特征的scale,re-scaled的金字塔可以用一个4-d的tensor表示:$\mathcal{F} \in \mathcal{R} ^{L\times H\times W\times C}$。$L$表示特征金字塔的层数,$H$、$W$、$C$分别表示height、weight、channel。进一步定义$S=H\times W$将tensor reshape成3-d的表示:$\mathcal{F} \in \mathcal{R} ^{L\times S\times C}$。
给定特征张量 $\mathcal{F} ∈ R^{L\times S\times C}$ ,应用自注意力的一般公式为:
$ \pi(\cdot ) $简单实现注意力的方式是直接使用全连接层学习所有维度的attention,表示注意力方法。但是这会带来庞大的计算成本。所以作者提出将attention分为三个连续的attention:
Scale-aware Attention
根据语义重要性动态融合不同尺度的特征:
$f(\cdot)$是$1\times 1$卷积的线性函数,$\sigma(x)=max(0,min(1,\frac{x+1}{2}))$是hard-sigmoid function。
Spatial-aware Attention
基于融合特征的空间感知注意模块来关注空间位置和特征级别之间一致共存的判别区域:
$K$表示稀疏采样的位置数量。模块不是对所有空间位置都进行注意力计算,而是选择一些关键的采样位置进行关注。$p_k+\Delta p_k$是通过自学习的空间位移量 $\Delta p_k$ 偏移后的位置。这个位移量帮助注意力模块更好地聚焦在判别性区域上。$\Delta m_k$是一个自学习的重要性标量,用于表示在位置$p_k$上的特征的重要性。这些标量也是从输入特征$\mathcal{F}$中通过注意力机制学习到的。
Task-aware Attention
任务感知注意力通过学习控制阈值的超函数$[\alpha^1,\alpha^2,\beta^1,\beta^2]^T=\theta(\cdot)$动态调整通道,具体操作是使用一个全局平均池化对$L\times S$维降维,然后使用两个全连接层和一个归一化层,最后应用移位的sigmoid函数对输出进行归一化$\left [ −1, 1 \right ] $,$\mathcal{F}_c$表示第$c$个通道的特征切片。
最后,由于上述三种注意力机制是顺序应用的,因此可以多次嵌套公式2。如图一所示。
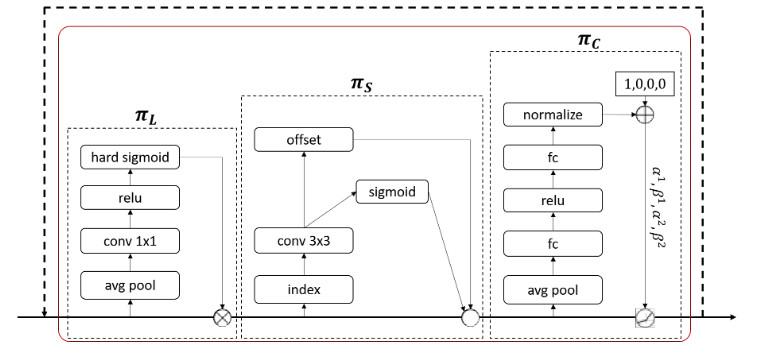
图一
Generalizing to Existing Detectors
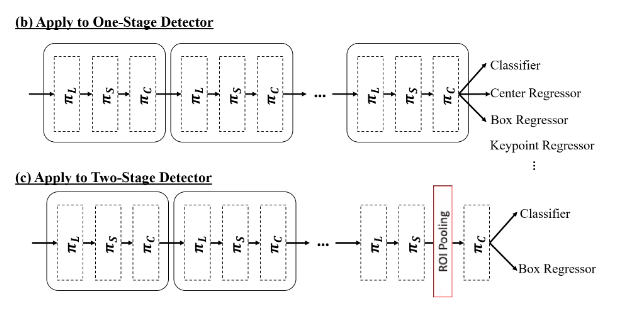
图二
如图二所示,对于One-Stage检测器,由于我们多重注意力机制的优势,可以同时应用于分类和回归等多个任务,只需要将各种类型的预测附加到Dynamic head的尾部。
Two-Stage检测器使用RPN和ROI层从主干网络的特征金字塔中提取中间表示,为了配合这一特性,首先在 ROI 池化层之前将尺度感知注意力和空间感知注意力应用到特征金字塔上,然后使用任务感知注意力来替换原来的全连接层,如图 2 © 所示。
我很可爱,请给我钱
- 本文链接: https://ajian.one/2024/08/09/论文阅读:Dynamic-Head-for-Object-Detection/
- 版权声明: 本博客所有文章除特别声明外,均默认采用 CC BY-NC-SA 4.0 许可协议。




